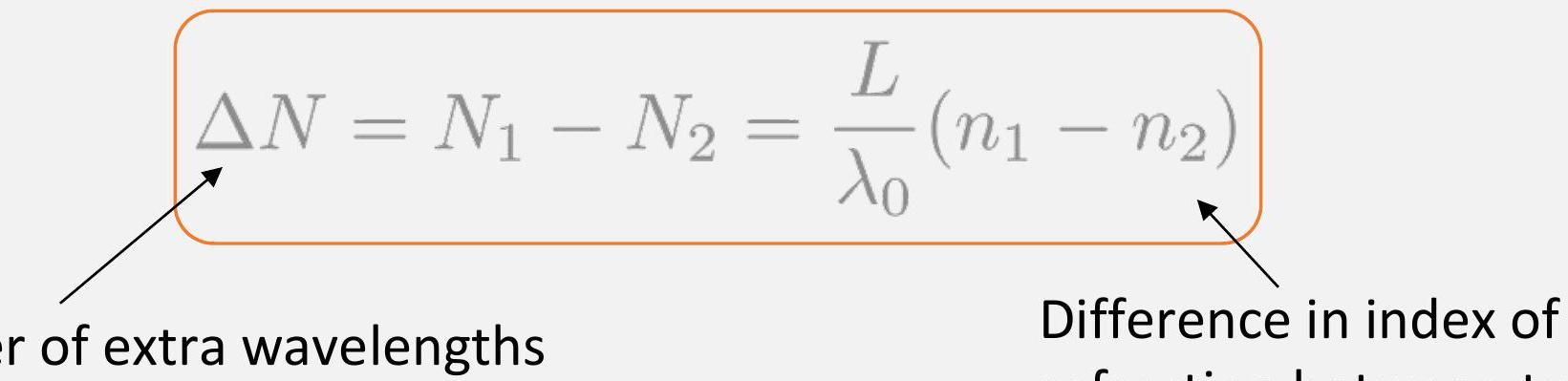实验 5：干涉仪

实验物理学导论 <br>物理学 UN 1494

谢瓦莉 <br>vh2289@columbia.edu <br>办公时间：每周五上午10点至11点，Pupin 413

展望

• 实验 5：干涉仪
• 下周没有实验
• 下周没有讲座
• 实验 5 报告将在春假后一周提交

大纲

• 背后的物理学：
  • 电磁波
  • 介质中的电磁波：反射与折射
  • 干涉学：
    • 迈克耳孙干涉仪
    • 法布里-佩罗干涉仪
  • 实验内容：
    • 介绍实验装置
    • 使用每种干涉仪分别测定氦氖激光的波长λ
    • 测量空气的折射率

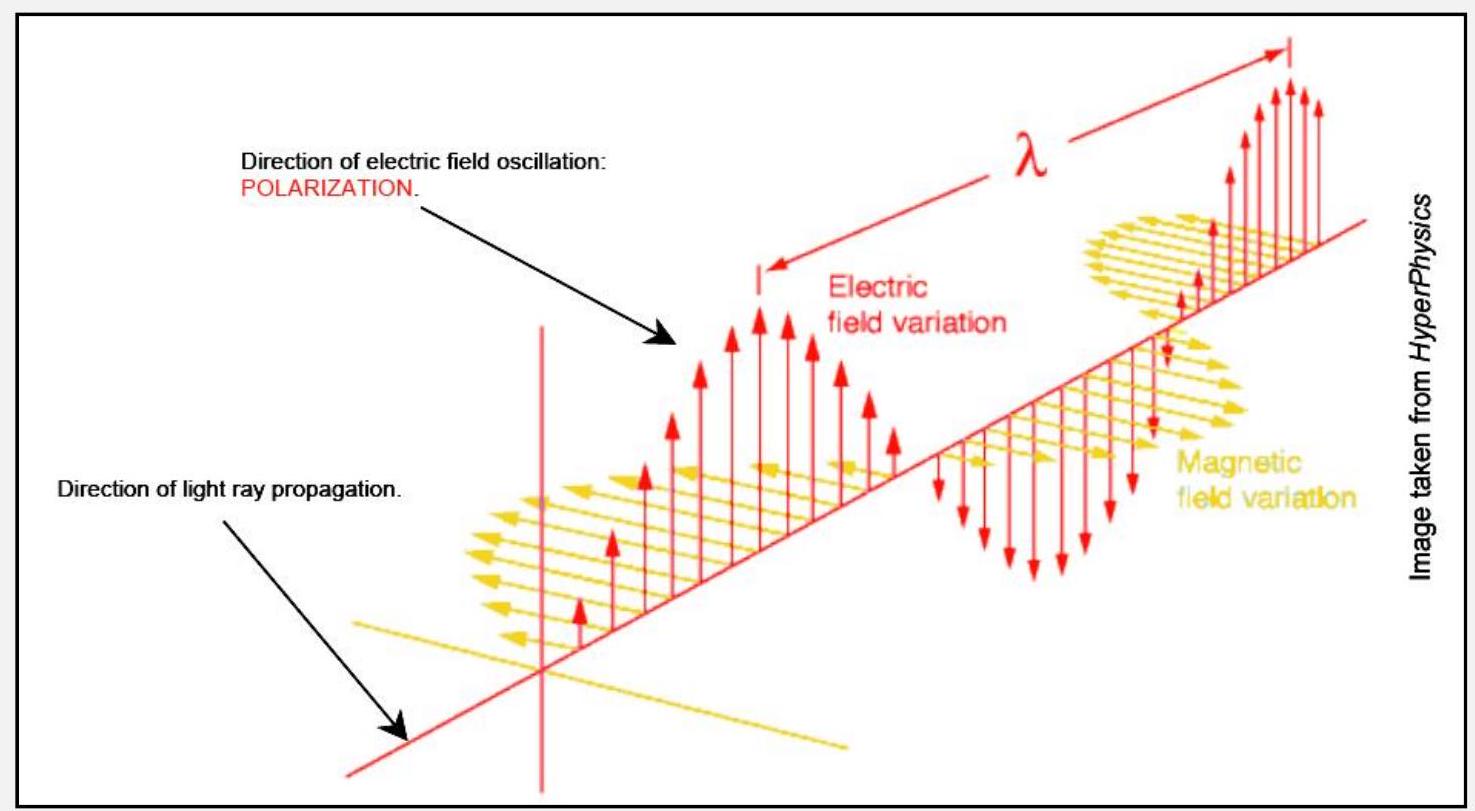
电磁波

• 电磁波 = 振荡的电场和磁场
• 电磁波在真空中的传播速度为光速

$$c=299792458 \, \mathrm{m/s} \simeq 3 \times 10^{8} \, \mathrm{m/s}$$

• 电场和磁场总是相互垂直的 (詹姆斯·克拉克·麦克斯韦……非常聪明的人...)

干涉=波叠加

• 波动的一个基本特性是可以与其他波叠加
• 这种叠加的结果可能导致波的幅度增大或减小
• 这个现象叫做干涉

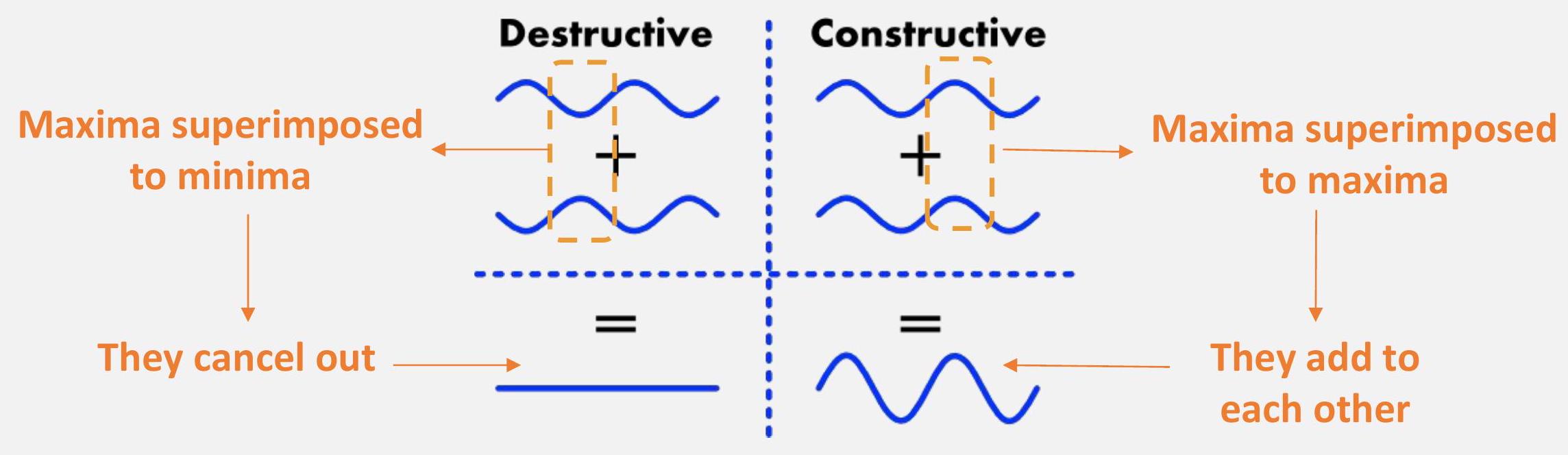
干涉=破坏性干涉+建设性干涉

破坏性干涉=最大值叠加到最小值=它们相互抵消

建设性干涉=最大值叠加到最大值=它们相互叠加

Destructive INTERFERENCE=max+min=0

Constructive INTERFERENCE=max+max=min+min=2|A|

破坏性干涉Destructive INTERFERENCE=0

Constructive INTERFERENCE=2maxima

• 在这个实验中，我们将研究光的波动特性，特别是干涉现象
• 电磁波可以以建构性或破坏性的方式叠加

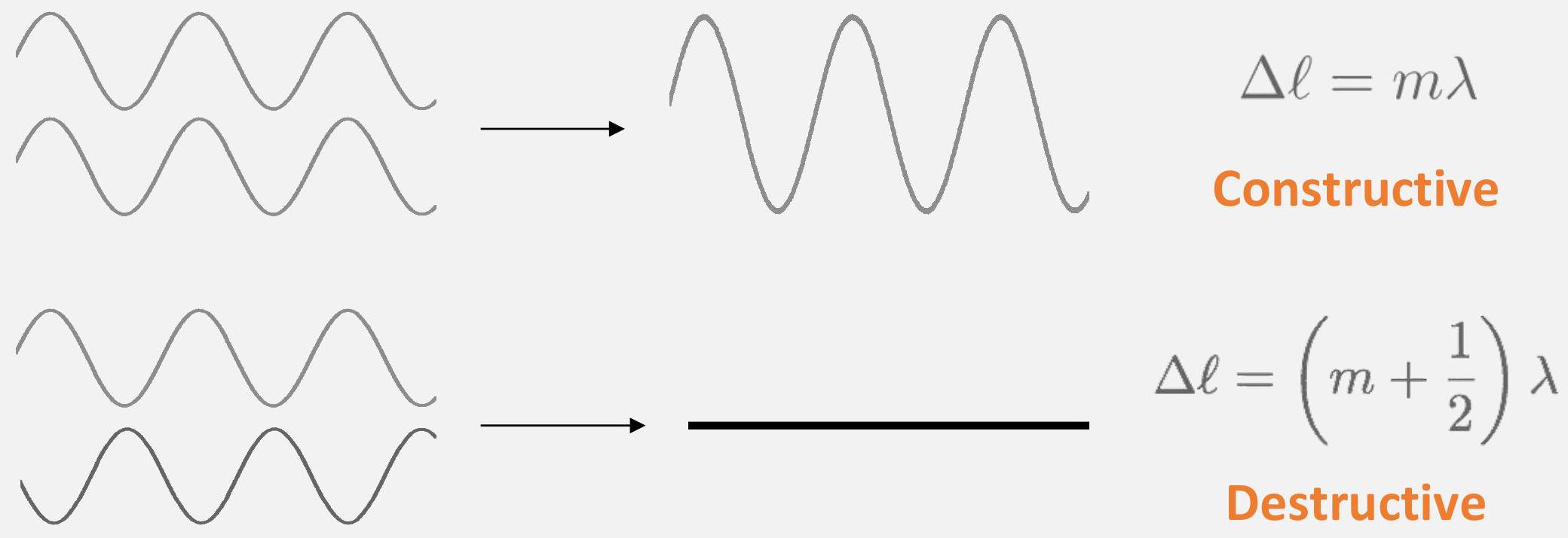
条件干涉公式

建设性干涉（Constructive Interference）=对准=叠加=亮点

$$\Delta l = m\lambda$$

破坏性干涉（Destructive Interference）=错位=相消=暗点

$$\Delta l = \left( m + \frac{1}{2} \right) \lambda$$

• 因此，典型的干涉图样看起来像这样：

波动干涉

• 干涉可以由以下原因引起：
  • 路径长度差异
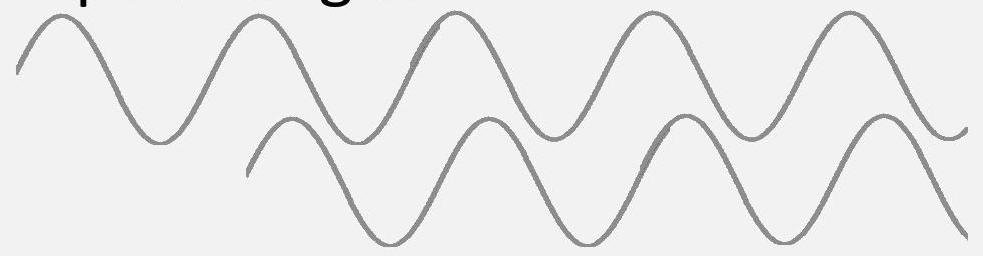
  • 初相位差异
  • 波长差异
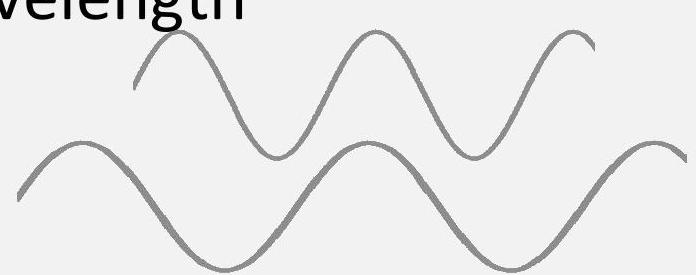
  • *介质差异（稍后会讲解）

介质中的电磁波

• 介质中的电场和磁场与在真空中的不同
• 微观解释：电介质（绝缘体）可以被电磁场极化。极化的介质反过来可以影响电磁场的性质
• 宏观描述：可以定义电位移场：

宏观描述（Macroscopic description） 可以定义一个 电位移场（electric displacement field）$\vec{D}$：

$$\vec{D} = \epsilon_0 \vec{E} + \vec{P}$$

• $\vec{D}$ ：电位移（Electric displacement）
• $\vec{P}$ ：极化（Polarization）

$$\vec{P} = \epsilon_0 \chi_e \vec{E}$$

• $\chi_e$ ：介质的电极化率（Susceptibility of the medium）

$$\Rightarrow \vec{D} = \epsilon_0 \epsilon_r \vec{E}$$

• $\epsilon_r$ ：相对介电常数（Relative permittivity）

对于大多数常见的介电材料，电位移与外加电场成正比：

For the most common dielectric materials, electric displacement is proportional to applied electric field.

• 一般来说，介质中的电磁学与真空中的电磁学不同
• 麦克斯韦方程发生变化：

真空中的方程：

$$\begin{aligned} \boldsymbol{\nabla} \cdot \mathbf{E} & =\frac{\rho}{\varepsilon_{0}} \\ \boldsymbol{\nabla} \cdot \mathbf{B} & =0 \\ \boldsymbol{\nabla} \times \mathbf{E} & =-\frac{\partial \mathbf{B}}{\partial t} \\ \boldsymbol{\nabla} \times \mathbf{B} & =\mu_{0} \mathbf{J}+\mu_{0} \varepsilon_{0} \frac{\partial \mathbf{E}}{\partial t} \end{aligned}$$

物质中的方程：

$$\begin{align*} \boldsymbol{\nabla} \cdot \mathbf{D} & =\rho_{f}  \tag{高斯定律}\\ \boldsymbol{\nabla} \cdot \mathbf{B} & =0 \\ \boldsymbol{\nabla} \times \mathbf{E} & =-\frac{\partial \mathbf{B}}{\partial t} \\ \boldsymbol{\nabla} \times \mathbf{H} & =\mathbf{J}_{f}+\frac{\partial \mathbf{D}}{\partial t} \end{align*}$$

（无磁荷） （法拉第定律） （安培定律）

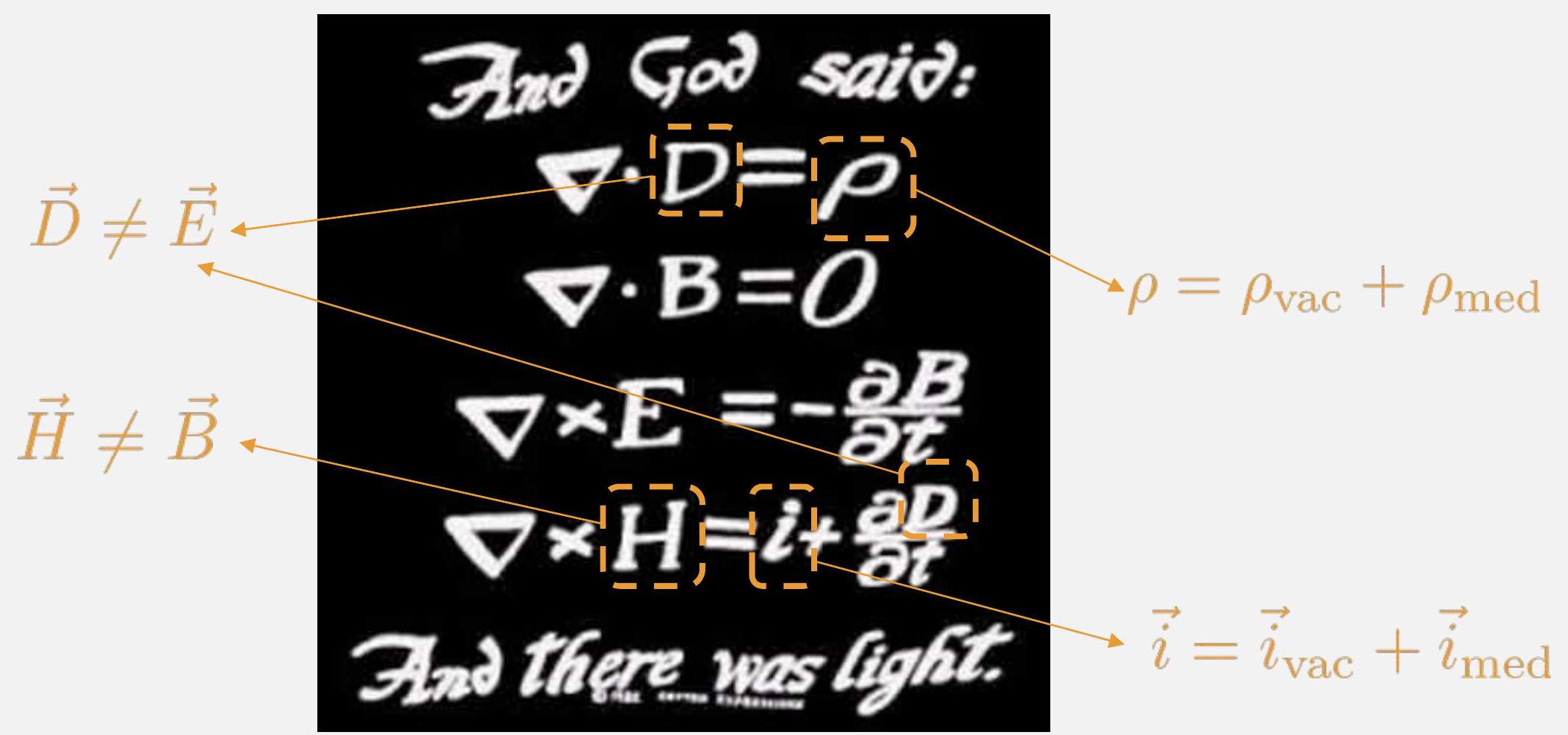
麦克斯韦方程组（Maxwell's Equations）

And God said:

$$\nabla \cdot \vec{D} = \rho$$

$$\nabla \cdot \vec{B} = 0$$

$$\nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}$$

$$\nabla \times \vec{H} = \vec{i} + \frac{\partial \vec{D}}{\partial t}$$

And there was light.

---

电磁场关系

• $\vec{D} \neq \vec{E}$ （电位移场 $\vec{D}$ 与电场 $\vec{E}$ 的区别）
• $\vec{H} \neq \vec{B}$ （磁场强度 $\vec{H}$ 与磁感应强度 $\vec{B}$ 的区别）

电荷密度

$$\rho = \rho_{\text{vac}} + \rho_{\text{med}}$$

（真空电荷密度与介质电荷密度的总和）

电流密度

$$\vec{i} = \vec{i}_{\text{vac}} + \vec{i}_{\text{med}}$$

（真空电流密度与介质电流密度的总和）

折射

• 问题：如果电磁波在真空和介质中的行为不同，那么这如何影响光的传播？
• 折射：光从一个介质进入另一个介质时发生弯曲（例如，从真空到空气，从空气到玻璃等）
• 光在两种材料之间的界面上的行为由斯涅尔定律描述：

$$n_{1} \sin \theta_{1}=n_{2} \sin \theta_{2}$$

$$\begin{array}{|l|l|} \hline n_{1} \sin \theta_{1}=n_{2} \sin \theta_{2} ; \\ n_{i}=\text{材料的折射率} \\ \hline n_{2} & \theta_{1} \\ \hline \end{array}$$

光程长度=光学路径长度

• 问题：折射率到底是什么？
• 由于麦克斯韦方程在介质中的不同，光速在介质中也不同！

$$\text{折射率} \equiv n=\frac{c}{v}$$

其中：$c=$ 真空中的光速 $v=$ 介质中的光速

• 后果：来自同一源的电磁波，但在不同的介质（即不同的折射率）中传播，在相同的物理距离上具有不同的光学路径长度

光学路径长度（OPL）

• 改变$\mathrm{OPL}=\int_{t_{1}}^{t_{2}} d t c=\int_{x_{1}}^{x_{2}} d x n(x)$的两种方法
  • 改变物理距离
  • 改变折射率（即将其放入不同的介质中）

---

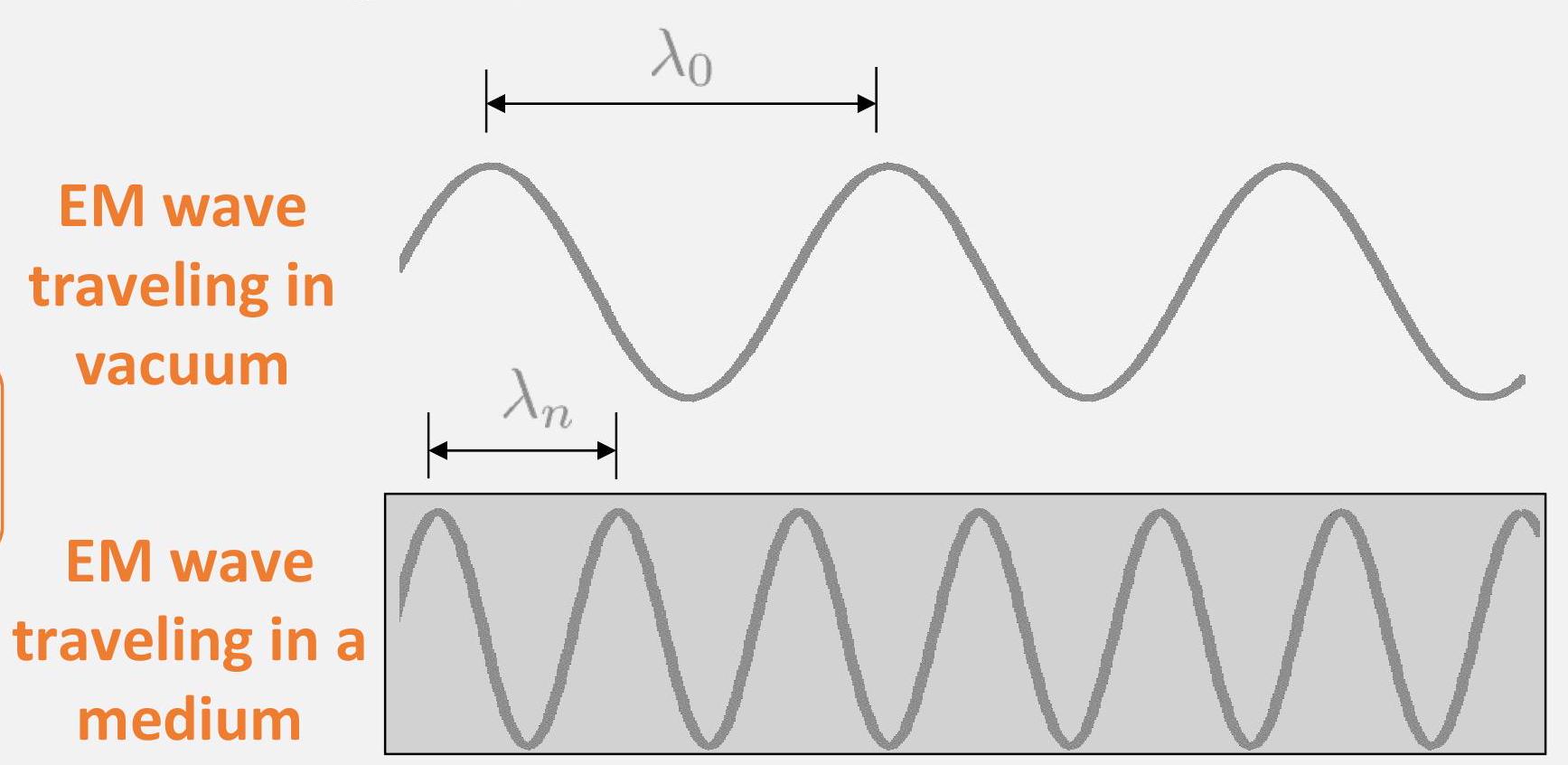
波长在介质中的变化 光在不同介质中传播时，其波长发生变化，满足以下关系：

$$\lambda_n = \frac{\lambda_0}{n}$$

其中：

• $\lambda_n$ 是光在折射率为 $n$ 的介质中的波长。
• $\lambda_0$ 是光在真空中的波长。
• $n$ 是介质的折射率。

物理意义：

• 当光进入折射率更高的介质（$n > 1$）时，波长变短。
• 当光回到真空或低折射率介质时，波长变长。
• 光的频率 $f$ 不变，但波长变化，满足波速公式：

$$v = \frac{\lambda_n}{T} = f \lambda_n$$

在介质中，光速 $v$ 变为：

$$v = \frac{c}{n}$$

但频率 $f$ 保持不变，因此波长必须缩短。

这个公式在光学、激光、光纤通信等领域中非常重要。

不同介质中的OPL

• 为了研究干涉，我们只关心波之间的相位差（即波传播过程中额外的波长数）
• 假设两波分别在两个边长为$L$的盒子中传播，但这两个盒子分别填充了两种不同的介质（$n_{1}$和$n_{2}$）：

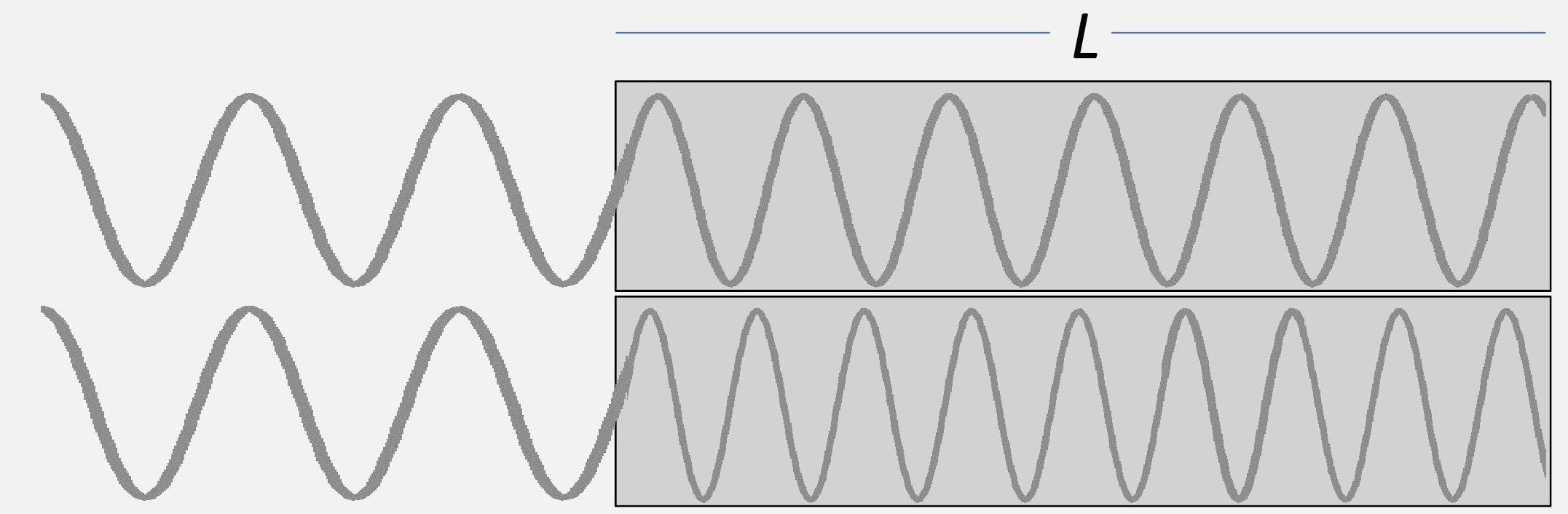
为了研究干涉，我们只关心波之间的相位差（即波传播过程中额外的波长数）

• 假设两波分别在两个边长为$L$的盒子中传播，但这两个盒子分别填充了两种不同的介质（$n_{1}$和$n_{2}$）：
• 每个盒子中包含的波长数将是：

$$N_{1}=\frac{L}{\lambda_{n_{1}}}=L \frac{n_{1}}{\lambda_{0}} ; \quad N_{2}=\frac{L}{\lambda_{n_{2}}}=L \frac{n_{2}}{\lambda_{0}}$$

• 因此，额外的波长数是：

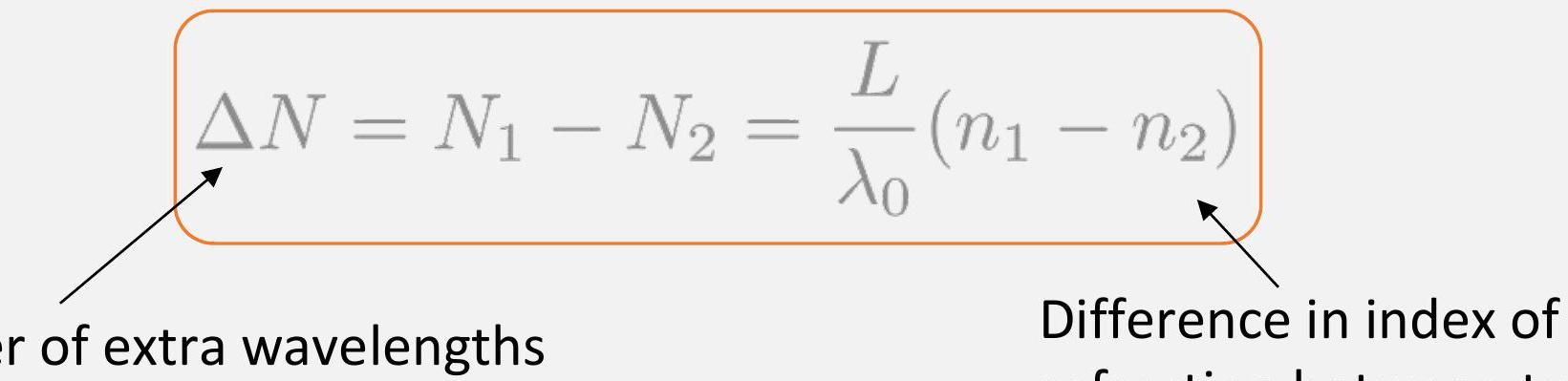
额外的波长数

两路径之间折射率的差异

光学相位差计算公式

$$\Delta N = N_1 - N_2 = \frac{L}{\lambda_0} (n_1 - n_2)$$

参数含义

• $\Delta N$：两个光学路径的相位差（Optical Path Difference, OPD）。
• $N_1, N_2$：分别表示光在不同介质 $n_1$ 和 $n_2$ 中传播的光学路径数。
• $L$：光传播的物理路径长度。
• $\lambda_0$：光在真空中的波长。
• $n_1, n_2$：分别表示两种介质的折射率。

物理意义

• 该公式用于计算光在不同折射率介质中传播时的相位差。
• 折射率差 $(n_1 - n_2)$ 越大，相位差 $\Delta N$ 越大，意味着光波在两个介质中累积的相位不同，可能引起干涉效应。
• 在干涉实验（如迈克尔逊干涉仪）中，该公式常用于计算光程差引起的条纹移动。

这个公式在光学干涉、透射测量、折射率测量等领域广泛应用！

干涉仪Interferometry

• 干涉仪利用的是来自同一相干光源但具有不同路径长度的两束光的干涉
• 主要思想如下：

1. 从相同的相干光源开始（相同的 $\lambda$、极化、相位 $\phi$）
2. 将两束光分别导入不同的路径，路径长度差为$\Delta \ell$
3. 让这两束光在未来某个点重新汇聚

• 现在，这两束波可以根据以下条件进行建构性或破坏性干涉： $\Delta \ell=m \lambda ; \quad m=0, \pm 1, \pm 2, \ldots$ （建构性干涉） $\Delta \ell=(m+1 / 2) \lambda ; \quad m=0, \pm 1, \pm 2, \ldots$（破坏性干涉）

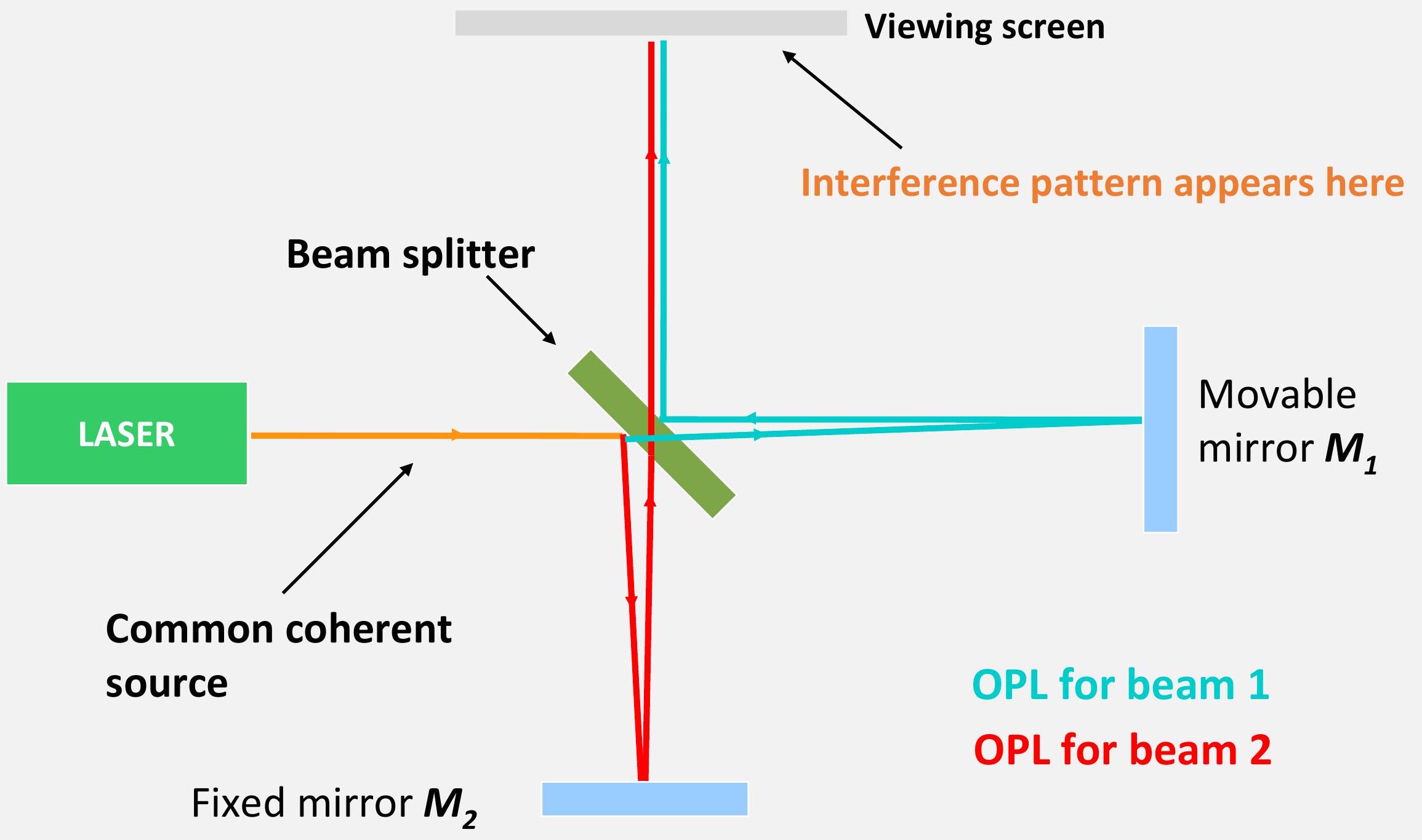
迈克耳孙干涉仪

1. 将单束光分成两束，然后重新合并。
2. 观察者可以看到投射到小屏幕上的干涉图样。
3. 通过移动其中一面镜子，观察者可以改变路径长度差 $\Delta \ell$，其结果是干涉图样发生偏移。

法布里-佩罗干涉仪

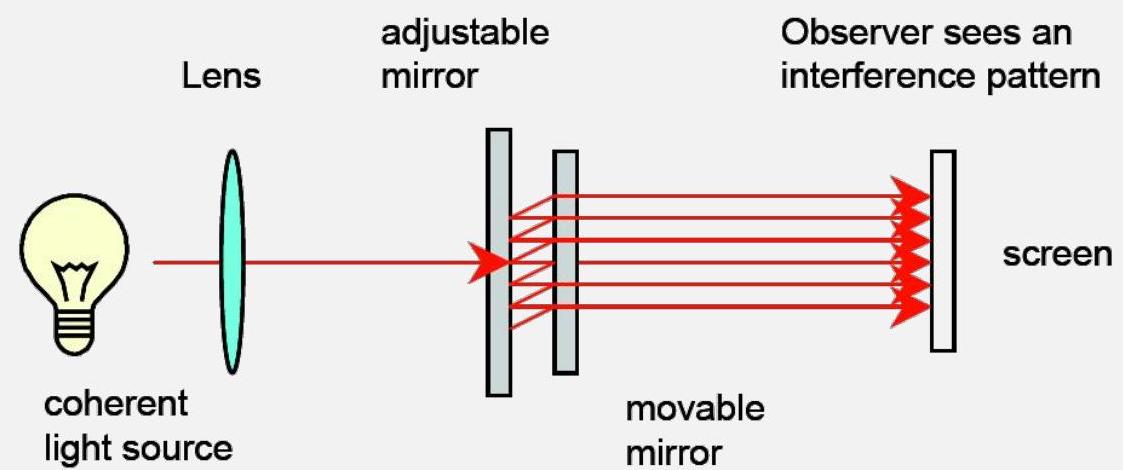
• 同样的思想：将光束分成两束，然后重新合并。
• 然而，不是仅仅将光束分成一次，而是利用镜面腔体多次分束。
• 每次反射都会增加一个小的路径长度差 $\Delta \ell$
• 最终的结果是一个圆形的干涉图样
• 主要优点：条纹更加明亮且容易区分

法布里-佩罗干涉仪

明亮条纹的条件（建构性干涉）

• 明亮条纹的存在条件对两种干涉仪都是相同的
• 假设我们从两束光处于相位相同开始并观察明亮条纹的位置，然后：

1. 修改其中一条路径长度 $\rightarrow$ 明亮条纹将不再是明亮条纹
2. 当总路径长度差为 $\lambda$ 时，它们将再次成为明亮条纹
3. 这将在 $2 \lambda, 3 \lambda$ 等处再次发生

• 一般来说，如果我们将其中一条路径改变 $d_{m}$，为了使明亮条纹回到原来的位置，我们必须有：

$$2 d_{m}=m \lambda ; \quad m=0, \pm 1, \pm 2, \ldots$$

实验目标

• 在本实验中，您将使用迈克耳孙干涉仪和法布里-佩罗干涉仪
• 法布里-佩罗干涉仪：
  • 测量氦氖激光的波长
• 迈克耳孙干涉仪：
  • 测量氦氖激光的波长
  • 测量空气的折射率 $\left(n_{\text {air }}\right)$。

法布里-佩罗（FP）干涉仪：设置

如何读取千分尺

• 千分尺将允许您将其中一面镜子移动非常小的距离。
• 这将导致干涉图样的移动

例子：在图片中，您可以读取到$500 \mu \mathrm{~m}$刻度，$25 \mu \mathrm{~m}$刻度，旋钮读数为$7 \mu \mathrm{~m}$。 位置 $=532$ $\mu \mathrm{~m}$

FP干涉仪：操作步骤

• 一些小贴士：
  • 转动千分尺旋钮来移动镜子会导致条纹图样的变化。
  • 条纹移动得非常快！可以请实验伙伴帮忙。
  • 测量至少20个条纹。测量的条纹越多，测量越精确！
  • 记录镜子移动的距离 $d_{m}$ 和穿过固定点的条纹数量。
  • 重复测量总共5次！

FP干涉仪：氦氖激光波长

• $d_{m}$ 与 $m$（条纹数量）之间的关系：

$$d_{m}=m\left(\frac{\lambda}{2}\right)$$

• 对每次测量，使用上述公式提取波长 $\lambda$。
• 报告平均值：$\bar{\lambda} \pm \sigma_{\lambda}$
• 与接受值632.8 nm进行比较

迈克耳孙干涉仪：设置

迈克耳孙干涉仪：操作步骤

• 移除激光前面的透镜。
• 设置小贴士：
  • 为了获得最佳效果，在放置透镜之前，请确保两束光几乎完全重合！
  • 与FP干涉仪相同的提示适用于迈克耳孙干涉仪。
• 测量氦氖激光波长：
  • 相同的操作步骤：测量条纹与可移动镜子距离的关系。进行10次试验。
  • 报告 $\bar{\lambda} \pm \sigma_{\lambda}$
  • 与接受值和法布里-佩罗干涉仪进行比较。

迈克耳孙干涉仪：测量 $\mathrm{n}_{\text {air }}$

• 通过改变压力来改变光的光学路径长度：

$$P_{\mathrm{atm}}, n_{\mathrm{air}} \longrightarrow P \ll P_{\mathrm{atm}}, n \simeq n_{\mathrm{vac}}=1$$

• 压力的变化导致折射率的变化。
• 注意：压力变化 $\Delta P$ 与折射率变化 $\Delta n$ 成线性关系。
• 迈克耳孙干涉仪的示意图设置如下：

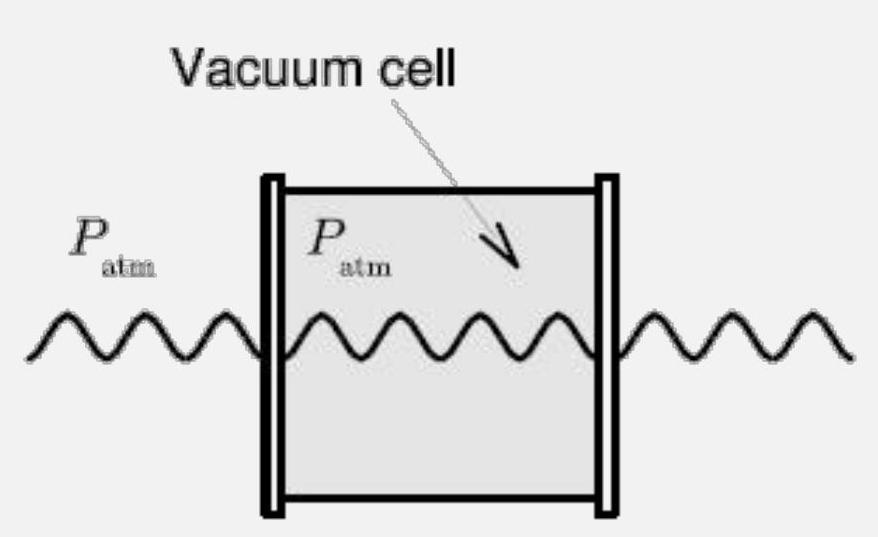
压力变化 = 折射率变化 $=$ 不同的波长

真空室与泵浦

迈克耳孙干涉仪：测量 $\mathrm{n}_{\text {air }}$

• 真空室最初处于 $P_{\text {atm }}$。
• 您将缓慢抽出空气以改变压力，并计算通过某一点的条纹数量。
• 在抽气时固定旋转指针，以防止真空室发生震荡/旋转。
• 一些压力计读取单位为 cm Hg；有些则以英寸 Hg 为单位读取。
• 单位换算不重要，因为我们只需要压力差（只要保持一致即可）。

计算折射率

• 我们已经看到，当折射率发生变化时，经过某一点的条纹数是由以下公式给出的：

$$m=\Delta N=\frac{2 d}{\lambda_{0}}\left(n_{f}-n_{i}\right)$$

• 问题：$n_{i}$ 和 $n_{f}$ 都是未知的。
• 解决方案：将一切除以压力变化：

$$n_{f}-n_{i}=\frac{m \lambda_{0}}{2 d} \Longrightarrow \frac{n_{f}-n_{i}}{P_{f}-P_{i}}=\frac{m \lambda_{0}}{2 d\left(P_{f}-P_{i}\right)}$$

• 假设：$\Delta n / \Delta P=\alpha=$ 常数
• 因此：

$$m=\frac{2 d \alpha}{\lambda_{0}}\left(P_{f}-P_{i}\right)$$

迈克耳孙干涉仪：计算 $\mathrm{n}_{\text {air }}$

• 至少进行 7 次测量 $m$ 和 $\Delta P$
• 通过以下公式将 $m$ 转换为 $\Delta n$：

$$\Delta n=n_{f}-n_{i}=\frac{m \lambda_{0}}{2 d}$$

• 注意：使用 $\lambda_{0}=632.8 \mathrm{~nm}$
• 绘制 $\Delta P$ 与 $\Delta n$ 的关系图：
  • 确定斜率 $\alpha$
• 现在使用 $P_{\text {atm }}=76 \mathrm{~cm} \mathrm{Hg}$，$P_{\text {vac }}=0, n_{\text {vac }}=1$ 计算 $n_{\text {air }}$：

$$n_{\mathrm{air}}=n_{\mathrm{vac}}+\alpha P_{\mathrm{atm}}$$

真空室中的折射率

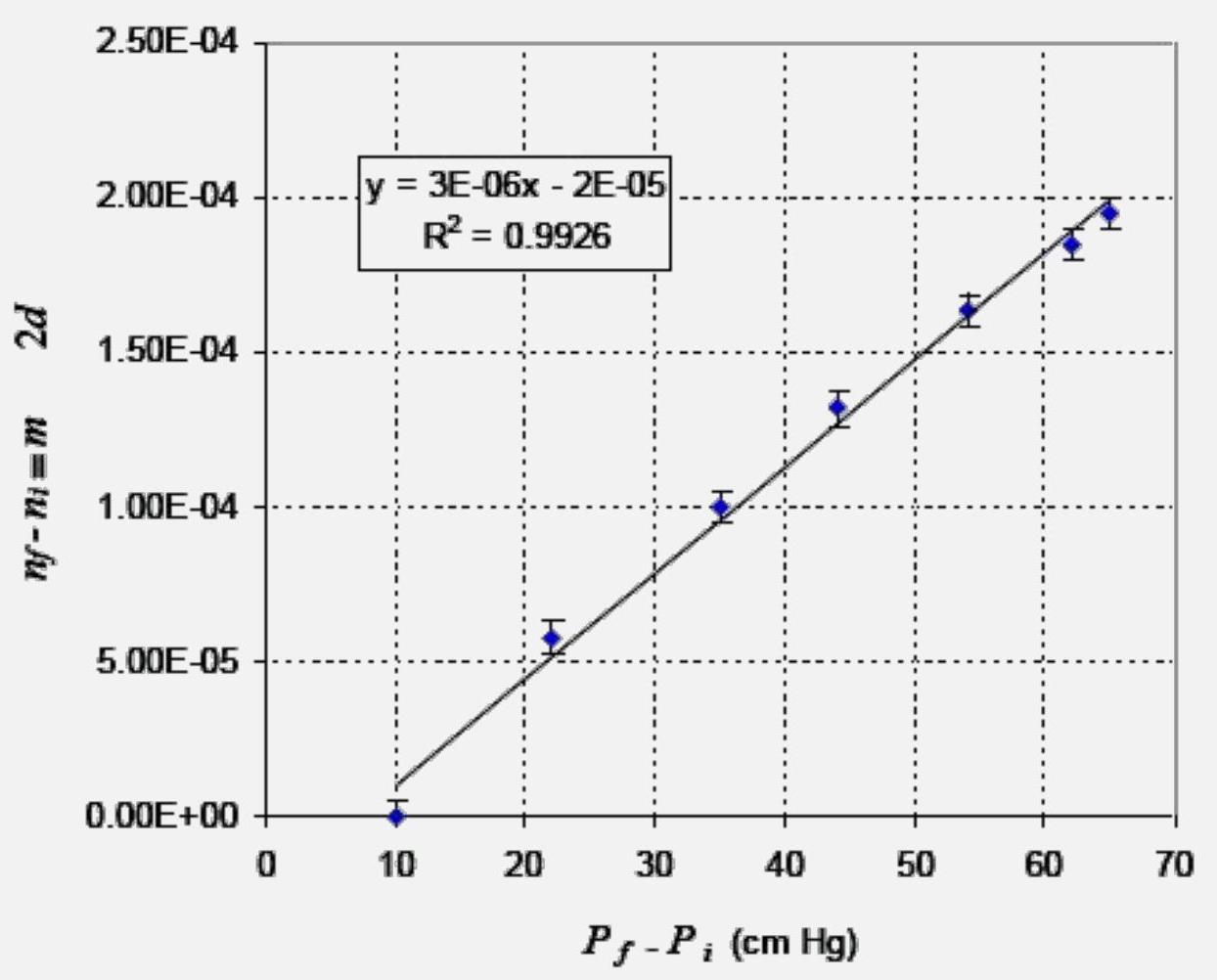
总结

• 通过使用迈克耳孙和法布里-佩罗干涉仪并改变光束的光学路径长度，我们可以测量系统的许多参数。
  • 氦氖激光的波长
  • 空气的折射率
• 这可能是整个学期中最困难和最繁琐的实验：需要准备充分才能进入实验室！！
• 尽管如此，这个实验具有很大的潜力来获取高质量数据并进行清晰的分析。

小贴士

• 您会注意到，中心的第一个条纹通常非常厚，而从第三个条纹开始它们非常细。最佳的计数条纹通常是第二个条纹。
• 两种干涉仪都非常精确，尤其容易受到环境振动的影响。在进行测量时，尽量减少振动，例如，避免触碰桌面。
• 最大的误差来源最有可能是误数条纹，因此请为误差分配一个合理的大误差（而不是取根号N！）

小贴士

• 在获取不同数据时，总是从零开始计数。这将避免传播错误计数的条纹。
• 使用千分尺时，最好从 $500 \mu \mathrm{~m}$ 的刻度开始测量（线性响应）。每次都从那里重新开始！还要注意反向间隙！
• 请小心处理真空室、镜子和透镜，只触摸其边缘，以防留下指纹！镜子和透镜上的指纹会影响实验结果。